Límite De Una Función
Es un concepto fundamental del análisis matemático aplicado a las funciones. En particular, el concepto aplica en análisis real al estudio de límites, continuidad y derivabilidad de las funciones reales.
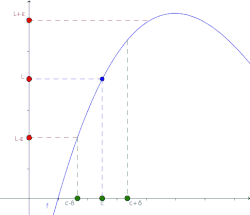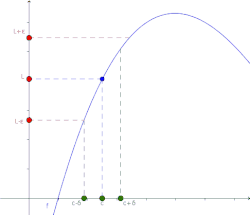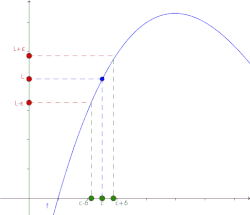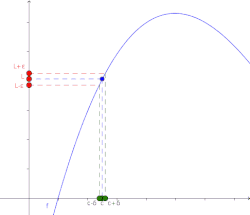
Intuitivamente, el hecho de que una función f alcance un límite L en un punto c significa que, tomando puntos suficientemente próximos a c, el valor de f puede ser tan cercano a L como se desee. La cercanía de los valores de f y L no depende del valor que adquiere f en dicho punto c.
El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo existe un tal que para todo número real x en el dominio de la función .
El límite de una función f(x), cuando x tiende a c es L si y sólo si para todo existe un tal que para todo número real x en el dominio de la función .
Esto, escrito en notación formal:
Lo importante es comprender que el formalismo no lo hacen los símbolos matemáticos, sino la precisión con la que queda definido el concepto de límite. Esta notación es tremenda mente poderosa, pues nos dice que si el límite existe, entonces se puede estar tan cerca de él como se desee. Si no se logra estar lo suficientemente cerca, entonces la elección del δ no era adecuada. La definición asegura que si el límite existe, entonces es posible encontrar tal δ.Esta es una formulación estricta del concepto de límite de una función real en un punto de acumulación ( o punto límite) del dominio de la función , se debe al matemático francés Luis Cauchy.5
Veamos un ejemplo. Supongamos que se quiere demostrar que El cálculo de este límite surge por simple sustitución, esto se debe a que la función afín es continua.
Límite secuencial
Consiste en definir al límite de una función en términos de los valores que toma para sucesiones contenidas en su dominio.
Una función real f tiene un límite L en un punto x = c de su dominio si para toda sucesión xn que converge a este punto c, la sucesión f(xn) converge a L.
En términos formales, si xn es una sucesión tal que
entonces f tiene límite L en x = c si y sólo si
lo cual se simboliza así:
Función que tiende a infinito[editar]
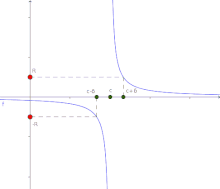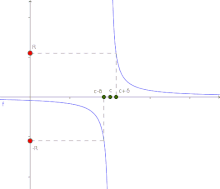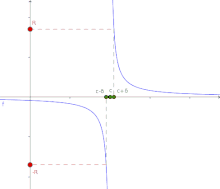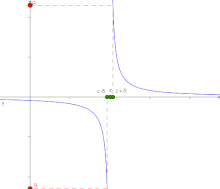
Si tomamos a la función f como una variable, por ejemplo, y, podemos utilizar la definición de variable que tiende a infinito, y combinarla con la definición de límite, de la siguiente manera. Dada cierta función f, diremos que tiende a infinito cuando crezca indefinidamente, a medida que nos acercamos a cierto punto c en el dominio. Esto equivale a afirmar que f no está acotada, para valores del dominio «suficientemente cercanos» a c. Esto se denota así , o también, se escribe .
El límite de una función f(x), cuando x tiende a c, es infinito si y sólo si para todo existe un tal que, para todo punto x en el dominio de f, se cumple .
Cuando una función tiende a infinito en un punto determinado c del dominio, la recta que determina la ecuación , es decir, todo punto de la forma , se denomina asíntota vertical de la función. Para el ejemplo dado, es la asíntota vertical.
El hecho de que no implica que sea posible la división por cero. Según la definición de este límite, , con lo cual, . En definitiva, es decir, está expresión es indefinida.
Tomemos otro ejemplo, la función logaritmo natural.
Recurrimos al límite lateral ya que el logaritmo sólo está definido para en los reales.
A medida que tomamos M cada vez más grande, podemos establecer R de modo que f supere a M en valor absoluto cuando lo hace x, con respecto a R.






 En términos formales, si xn es una sucesión tal que
En términos formales, si xn es una sucesión tal que
















No hay comentarios:
Publicar un comentario